Страница 1 из 1
задача: геометрия

Добавлено:
Пн дек 24, 2007 3:14 pm zavkhoz
Известно, что сумма расстояний от любой внутренней точки равностороннего треугольника до его сторон есть константа.
Докажите...

Добавлено:
Ср дек 26, 2007 5:54 pm Таня
ответ:const=корень из 3 разделить на 2 и умножить на сторону,правильно?

Добавлено:
Ср дек 26, 2007 6:00 pm zavkhoz
Таня писал(а):ответ:const=корень из 3 разделить на 2 и умножить на сторону,правильно?
если это sin(pi/3) то пожалуй что да

но в задаче требуется не вычислить, а доказать!

Добавлено:
Ср дек 26, 2007 6:20 pm Таня
Наглядно док-ся с рисунком,как я тебе тут треугольник изображу?

Добавлено:
Ср дек 26, 2007 8:26 pm Таня
Док-во напишу здесь,рисунок с буквами по почте,сможешь,вставишь.
Дано
АВС-треугольник
О-произвольная точка
ОF,OL,OK-расстояния от О до сторон АВ,АС,ВС соответственно
док-ть,что OF+OK+OL=cconst?при любых ОF,OL,OK
LM=OS(надеюсь это объяснять не надо,долго),след.
из тр.OKS
OK=LMsin60
OL=MS
из тр. MSC
OL=MS=MCtg60=AZtg60(из тр.AZP)
OF=LZsin60 (LZ=OР,рассм.тр.OFP)
OF+OK+OL=LZ√3/2+LM√3/2+AZ√3=(LZ+LM+2AZ)√3/2,
т.к.AZ=MC(из равенства для OL),то
OF+OK+OL=LZ√3/2+LM√3/2+AZ√3=(LZ+LM+2AZ)√3/2=(LZ+LM+AZ+MC)√3/2=AC√3/2,т.е.сторона на корень из 3 на 2,независимо от значений ОF,OL,OK.
Нужно вставит рисунок!!!!Так не поймёшь...

Добавлено:
Ср дек 26, 2007 10:59 pm whirl
Ох... гложат меня сомнения...
Я тут удаляю в поте лица всякий "кал" с форума, но теперь ....
т.к.AZ=MC(из равенства для OL),то
OF+OK+OL=LZ√3/2+LM√3/2+AZ√3=(LZ+LM+2AZ)√3/2=(LZ+LM+AZ+MC)√3/2=AC√3/2,т.е.сторона на корень из 3 на 2,независимо от значений ОF,OL,OK.
Что это????

Добавлено:
Ср дек 26, 2007 11:45 pm zavkhoz
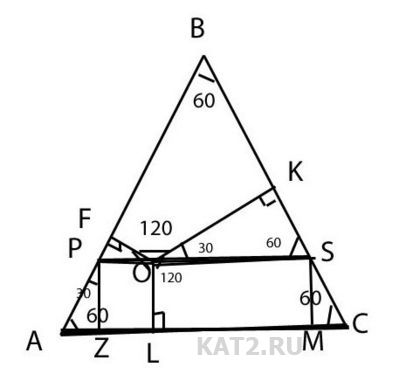
Таня писал(а):Док-во напишу здесь,рисунок с буквами по почте,сможешь,вставишь.
Дано
АВС-треугольник
О-произвольная точка
ОF,OL,OK-расстояния от О до сторон АВ,АС,ВС соответственно
док-ть,что OF+OK+OL=cconst?при любых ОF,OL,OK
LM=OS(надеюсь это объяснять не надо,долго),след.
из тр.OKS
OK=LMsin60
OL=MS
из тр. MSC
OL=MS=MCtg60=AZtg60(из тр.AZP)
OF=LZsin60 (LZ=OР,рассм.тр.OFP)
OF+OK+OL=LZ√3/2+LM√3/2+AZ√3=(LZ+LM+2AZ)√3/2,
т.к.AZ=MC(из равенства для OL),то
OF+OK+OL=LZ√3/2+LM√3/2+AZ√3=(LZ+LM+2AZ)√3/2=(LZ+LM+AZ+MC)√3/2=AC√3/2,т.е.сторона на корень из 3 на 2,независимо от значений ОF,OL,OK.
Нужно вставит рисунок!!!!Так не поймёшь...

Добавлено:
Чт дек 27, 2007 12:12 am demetrek
Таня писал(а):Док-во напишу здесь,рисунок с буквами по почте,сможешь,вставишь.
Дано
АВС-треугольник
О-произвольная точка
ОF,OL,OK-расстояния от О до сторон АВ,АС,ВС соответственно
док-ть,что OF+OK+OL=cconst?при любых ОF,OL,OK
LM=OS(надеюсь это объяснять не надо,долго),след.
из тр.OKS
OK=LMsin60
OL=MS
из тр. MSC
OL=MS=MCtg60=AZtg60(из тр.AZP)
OF=LZsin60 (LZ=OР,рассм.тр.OFP)
OF+OK+OL=LZ√3/2+LM√3/2+AZ√3=(LZ+LM+2AZ)√3/2,
т.к.AZ=MC(из равенства для OL),то
OF+OK+OL=LZ√3/2+LM√3/2+AZ√3=(LZ+LM+2AZ)√3/2=(LZ+LM+AZ+MC)√3/2=AC√3/2,т.е.сторона на корень из 3 на 2,независимо от значений ОF,OL,OK.
Нужно вставит рисунок!!!!Так не поймёшь...
Вроде логично, хотя доказаетльства таких типов помню меня учили доказывать методом "от противного". Попытался даказать. Пока какая-то фигня получается:)

Добавлено:
Чт дек 27, 2007 1:14 am zavkhoz
2 Таня:
+1 Сам доказал примерно таким же способом, на что мне показали простое и красивое док-во.
2 demetrek:
хотел дать другое доказательство, красивое и гораздо короче, но вовремя вклинился.
Пока не дам


Добавлено:
Чт дек 27, 2007 12:02 pm Таня
Короткое док-во
Использую тот же рис.
соединим точку О с вершинами А,В,С
Имеем 3 треугольника АОС,АОВ,СОВ с высотами OL,OF,OK
Сумма площадей этих тр. =соnst=площади тр. АВС,т.е.
1/2AC OL+1/2AB OF+1/2BC OK=const,т.к. у равност. тр. все стороны равны,след.АС=ВС=АС,тогда получаем
OL+OF+OK=const умножить на 2 и разделить на сторону=const,ч.т. доказать

Добавлено:
Чт дек 27, 2007 10:57 pm zavkhoz
Класс! +1


Добавлено:
Чт дек 27, 2007 11:08 pm Таня
А у тебя что за док-во,Петь?

Добавлено:
Пт дек 28, 2007 10:32 am zavkhoz
Такое же как у тебя
